What Is The Derivative Of In x? Get All Your Answers Here

The natural logarithm of an integer x is the logarithm to the base e, where e is the mathematical constant 2.718. It is typically expressed using the shorthand notation ln x rather than log ex, as you might anticipate. In exponential decay issues, logarithms are there to solve for the half-life, decay constant, or unknown duration. They are used in finance to address issues requiring compound interest and are essential in many fields of mathematics and science.

The differentiation formulae for exponential functions and their inverse functions, known as logarithmic functions, are as follows: It is worth noting that the exponential function f( x) = e x has the unique characteristic of having its derivative by the function itself, f′( x) = e x = f. ( x).

If you want to know more about this topic, you’re welcome here. Read on as we explore all the facts about derivations of (x).

Definition of In

The natural log is the inverse of e, which is a fancy way of saying the opposite. In terms of terminology, the Latin name is logarithmic natural, which yields the abbreviation ln. So, what exactly does inverse or opposite mean?

Ex. it allows us to fill in time and obtain development. We can use ln(x) to put in growth and obtain the time it would take.

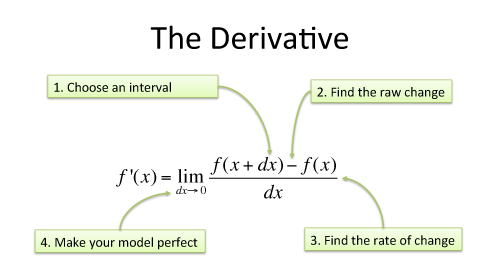
Functions of Derivative

A derivative is also a contract between two or more parties, the value of which is determined by an agreed-upon underlying financial asset, index, or security.
Common derivatives include futures contracts, forward contracts, options, swaps, and warrants.
Derivatives can be used to either minimize risk (hedging) or to take risk in exchange for a corresponding return (speculation).

Derivative of In (x) by the first principle

How can I use the first principle to find the derivative of x^x?

f(x)=xx

f′(x)

=limh→0f(x+h)−f(x)h

=limh→0(x+h)x+h−xxh

=limh→0(x+h)x+h−(x+h)x+(x+h)x−xxh

=limh→0(x+h)xlimh→0(x+h)h−1h+xxlimh→0(1+hx)x−1h

=limh→0(x+h)xlimh→0(x+h)h−1h+xxlimh→0(1+hx)xh⋅h−1h

=xxlnx+xxlne

=xxlnx+xx

=xx(lnx+1)

Derivative of In (x) square

We may be conditioned to believe that only positive values of x are acceptable for logarithm functions. Because x is squared, both positive and negative values of x are permitted for ln x2. The only restriction on x is that x = 0.

The slope of the tangent line at a point called the derivative. The slope of the tangent line will be positive if x > 0. For instance, at x = 2:

Similarly, from a graphical standpoint, tangent lines have a negative slope for x 0. Take a look at the tangent line at x = -2:

As a result, the derivative of ln x2 must agree with these findings. There are two simple methods for calculating the derivative of ln x2:

Making use of the chain rule
Using logarithmic properties

Both techniques rely on the assumption that the derivative of ln x = 1/x.

The Steps to Calculate

Let’s take a closer look at our first technique, the chain rule. What is the chain rule, and how does it work? To begin with, the chain rule is a formula for determining the composition of two or more functions. Assume we have a function with a complex parameter, such as sin x2. Sine is the function, and x2 is the input. If the input were merely x, we’d divide sin x by cos x to obtain cos x.

To use the chain rule, suppose that the function has a simple argument and write the derivative. The derivative of sin x2, in this case, is cos x2. Then we multiply by the argument’s derivative. 2x is the derivative of x2. Using the chain rule, the derivative of sin x2 is cos x2 multiplied by 2x, or simply 2x cos x2.

Chain rule

Because 1/x is the derivative of ln x, the derivative of ln x2 is 1/x2 times the derivative of x2:

The derivative of x2 is thus 2x:

Step 2: 1/x2 times simplify 2x may be expressed as 2x/x2.

Getting rid of the popular x term:

Let us now consider our second technique, the properties of logarithms, which are essentially the qualities or features of exponents.

Now you can implicitly take the derivative of both sides. You have to do it with respect to x, remembering to multiply by dy/dx on the left-hand side since it is given in terms of y, not x.

e^y dy/dx = 1

From the inverse definition, we can substitute x in for e^y to get

x dy/dx = 1

Finally, divide by x to get

dy/dx = 1/x

Thus proving the theorem.

Derivative of In (x) proof

The proof of this statement is not required for the AP Calculus course. But we feel that as long as proof is available, there is always something to learn from it. In general, it’s a good idea to need evidence or explanation for the theorems you learn.

From the inverse definition, we can substitute x in for e^y to get

x dy/dx = 1

Finally, divide by x to get

dy/dx = 1/x

Thus proving the theorem.

What is log x?

Before we move on to calculate the derivative of log x, let us define “log.” The term “log” refers to a common logarithm. It is, thus, a logarithm of base 10. If no base is specified for “log,” the default base is 10. Log = log10, for example. We may find the derivative of log x with respect to x using the techniques shown below.

But we will also be making use of the first principle.

We also will be making use of implicit differentiation.

You’ll find us using the ln x derivative.

Here, we will not only obtain the derivative of log x (with base 10) but also the derivative of log x with any base.

Derivative of log x

The log x derivative (log x with base a) is 1/ (x ln a). The noteworthy point here is that “ln” appears in the derivative of “log x.” It is worth noting that “ln” is known as the natural logarithm (or) a logarithm with base “e.” In other words, ln = loge. Furthermore, the derivative of log x is 1/(x ln 10) since the log’s default base is ten if no base is specified.

The log x (base 10) derivative with respect to x is represented by d/dx (log x) or (log x)’.

d/dx(log x) (or) (log x)’ = 1/(x ln 10)

d/dx(logₐ x) (or) (logₐ x)’ = 1/(x ln a)

Because the derivative of log x comes immediately from the derivative of log x, proving the latter is sufficient. In the next sections, we will demonstrate this formula using several techniques.

Derivative of In (x) absolute value

This section will also teach you how to calculate the derivative of an absolute value function.

Assume that |f(x)| is the absolute value function.

Let us calculate the derivative of |x| using the formula.

|x|’ = [x/|x|]. (x)

[x/|x|] = |x|’ .. (1)

|x|’ = x/ |x|

As a result, the derivative of |x| is

|x| x / |x|

Let y equal |x|’.

The result is y = x/|x|.

If we insert x = 0 into y = x/|x|, the denominator becomes zero.

At x = 0, y becomes undefined since the denominator becomes zero.

Let us try several other values for “x” in y.

When x = -3, y = -3/|-3| = -3/3 = -1.

Then x = -2, y = -2/|-2| = -2/2 = -1.

When x = -1, y = -1/|-1| = -1/1 = -1.

But x equals 0, y equals 0/|0| = 0/0 = undefined

When x = 1, y = 1/|1| = 1/1 = 1.

Then x = 2, y = 2/|2| = 2/2 = 1.

When x = 3, y = 3/|3| = 3/3 = 1.

Let us summarize the above calculation in a table. Then from the table, we can come to a conclusion.

Explanation using graphical definition

We may explain this by using the graphical definition of derivative, which is the slope of the graph at a given location (a derivative of x).

So, if you plot the graph of |x|, you’ll notice that there are only two potential slopes: +1 when x is positive and -1 when x is negative. (Note: the slope cannot be defined at 0).

As a result, a simple method to describe this in an expression is |x|/x, which returns 1 when x is positive and -1 when x is negative. Furthermore, We cannot calculate its value at 0.

As a result, the derivative of x’s absolute value is abs(x)/x.