Teaching your college students the way to divide fractions may be simply as easy as coaching multiplication… as soon as you already know all the little hints to get the proper solution. But — as with all math concept — while you educate department, you do not need your college students to simply resolve a trouble. You need them to recognize what is taking place in every question. But, it really is the thing.
It’s hard to get them to recognize dividing fractions in case you do not pretty get it yourself. We have been a chunk pressure data the subject, too. That’s why we appeared into the satisfactory equipment and simple methods to make certain your magnificence understands the important thing ideas for dividing fractions. Pay near attention, and through the stop of this text you’ll be a completely equipped, extremely assured fraction department master.
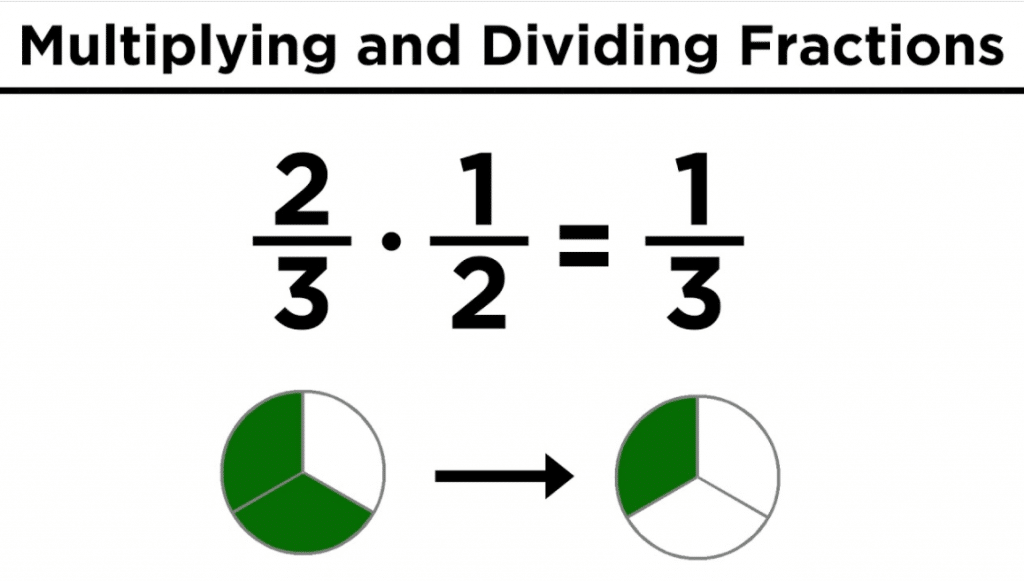
How dividing fractions works
Teaching college students the way to divide fractions is a part of the Common Core State Standards for Mathematical Practice. One of the maximum treasured matters to educate your college students while dividing fractions is what the solution manner. Take a examine the instance below:
½ ÷ ⅙ = three Why is the answer larger wide variety than the fractions involved? When you divide a fragment, you’re asking what number of groups of the divisor (2ndwide variety) may be located within side the dividend (first wide variety). For the above equation, we’re asking what number of ⅙ seem in ½.Imagine the instance equation as a cake. You’ve were given1/2 of of the cake remaining. If every serving of the cake is ⅙ of the whole, what number of servings do you’ve got got left?
How to divide fractions
If you actually divided fractions such as you have been dividing a ordinary math trouble, you’d extra than probable create a few complicated fractions and feature some thing that appear just like this:
That’s now no longer precisely an clean manner to follow. Luckily, there’s a shortcut you may use that makes dividing fractions tons simpler. You can resolve maximum department troubles through following those 3 steps:
- Flip the divisor right into a reciprocal
- Change the department signal to a multiplication image and multiply
- Simplify your solution if possible
Step 1: Flip the divisor right into a reciprocal
A reciprocal is what you multiply various through to get the price of one. If you need to alternate into one thru multiplication you want to multiply it through 0.5. In fraction shape this seems like:
²⁄₁ × ½ = 1To discover the reciprocal of a fragment you actually turn the numbers. The denominator will become the numerator and vice versa. Take a examine the instance equation again:
½ ÷ ⅙ = ?The first step to resolve the trouble is to show our divisor, ⅙, right into a reciprocal.
⅙ → ⁶⁄₁
Step 2: Change the department signal to a multiplication image and multiply
Dividing and multiplying are opposites of every other. When you create a reciprocal of various, you’re developing its contrary as well. In a department trouble, while you switch the divisor right into a reciprocal, you furthermore might want to alternate the equation from department to multiplication. Now that you’ve located the reciprocal of your divisor, you may alternate the equation from department into multiplication.
½ ÷ ⅙ = ? → ½ × ⁶⁄₁ = ?We’ve were given an intensive manual on the way to multiply fractions, however here’s a short tutorial:
- Multiply your numerators to get your new numerator
- Multiply your denominators to get your new denominator
- Simplify the very last fraction, if possible
For the instance equation you’ve got got troubles to resolve:
1 × 6 = 6 2 × 1 = 2 ½ × ⁶⁄₁ = ⁶⁄₂Now you are equipped to simplify to get the very last solution!
Step three: Simplify your solution if possible
Fractions characterize part of a whole. This manner many fractions constitute the equal price, so why now no longer make the fraction as easy as possible? For example, you nearly by no means say 5-tenths or ⁵⁄₁₀. Instead, you simplify that to one-1/2 of or ½.To get a fragment right all the way down to its most effective shape, you divide the numerator and denominator through their finest not unusual place issue. The finest not unusual place issue in ⁵⁄₁₀ is 5. Dividing each numbers down through 5 leaves you with ½.