Ground state electron definition

Atoms have an ideal configuration of their surrounding electrons. The ground-state electron configuration tells us which orbitals are going to be present in a given atom.

However, the ground-state electron configuration tells us the lowest possible energy configuration for an atom or a molecule. Now, this is the reason why its name is the ground state. It is the lowest level of energy we can have. However, this configuration is ideal for the atom. However, It is the easiest electron configuration to maintain. Now, the position of the electrons in our atom tells us lots of information about their atom structure. Now, we know what the ground state is, and we have a brief idea about it.

The ground state configuration of an atom

However, a silicon atom has 14 protons, neutrons, and electrons in its neutral state. Next, we need to find out in what orbitals does silicon places its electrons.

Ground state electron configuration rules

Aufbau principle

The Aufbau principle is the first rule of ground-state electron configuration. Now, we must place our electrons in the lowest energy states first and then work up to the higher energy states. Then our lowest ground state is the 1s orbital. Next, in our first column, let’s write the energy levels 1 2 3 4 5. Then, in the first row, we write the orbital names, which go s,p,d, then f. An s orbital can hold 1 set of spin paired electrons, the p orbitals can hold three sets of spin paired electrons. However, the f orbitals hold five sets of spin paired electrons. At last, the d orbital can hold seven sets of spin paired electrons(14 electrons). However, s is just a sphere around our nucleus. P orbitals have three configurations that look like dumbbells.
Each dumbbell shape can hold 2 electrons; that’s why we say the p orbitals can hold 6 electrons. Next, the highest arrow has the lowest energy and near the arrowhead is the highest energy. However, there are sometimes a few exceptions to this rule.
If we did have to go as high as 4s, then we can see that according to the Aufbau principle, 4s is a lower energy state than 3d.

Pauli-Exclusion principle

The Pauli exclusion principle is the second rule of ground-state electron configuration. Atoms are spin pairs that mean each orbital can hold electrons with opposite spins. Now we need to add electrons into 1s. Next, with the help of Aufbau’s principle, we can add electrons to each of the energy lines.

Hund’s rule

Hund’s rule is the third rule of ground-state electron configuration. Now, we can give one electron to each orbital when we have equivalent energy orbitals. However, we find the noble gas with a lower number on the periodic table than the atom we have.

The ground-state electron configuration of elements

The ground-state electron configuration of Carbon

Carbon’s ground state configuration is the 1s2 2s2 2p2. All orbitals about an atom are regions where two paired electrons spend 95% of their time. However, these orbitals take many different shapes. Now, the reason they have different shapes is that we have a balance between the proton’s nucleus pulling the electrons in and the electrons repelling each other.

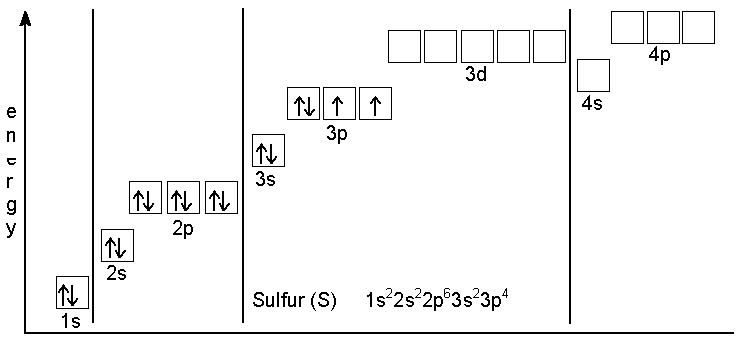
The ground-state electron configuration of Sulfur

The ground-state electron configuration is very easy, but it’s one of the most famous electron configurations. Sulfur is in the third row of the periodic table, and it’s the fourth element in the block. The atomic number of Sulfur is 16, which means a sulfur atom holds 16 electrons. Now list the atomic subshells in order of their increasing principal and azimuthal quantum numbers. However, to completely fill shells 1 and 2, we need 10 electrons. This means that those sex remaining electrons should be placed in shell 3. Shell 1 contains only one sub-shell. We can put only 2 electrons in those sub-shells.
Now, shell 2 includes the two subshells with 1s 2s orbital where we need to place the following two electrons. A 2p subshell with three 2p orbitals can accommodate a total of six electrons. Now we can start filling 3, and the first 2 electrons go into the 3s orbital. Next, the remaining four must be placed in 3p orbitals since their energy is lower than that of 3d orbitals out of the two possible arrangements of 3p electrons. However, we choose the one with two unpaired electrons.

The ground-state electron configuration of Nitrogen

7 is the number of protons, but it’s also the number of electrons. Nitrogen has 7 electrons, and we start with 1s. However, s orbitals can hold up to two electrons. So, we will put two for the number of electrons in the 1s orbital. Now we are down the 2s that will also hold two. Next, p can hold up to six electrons, but we need three more to complete the ground-state electron configuration for nitrogen. Now put 3 in that 2p orbital; we already have 2 plus 2 plus 3 that equals 7 electrons which is the number of electrons for the nitrogen. So, the configuration is 1s2 2s2 2p3.

The ground-state electron configuration of Oxygen

8 is the atomic number of oxygen. The atomic number equals the number of protons, but it also equals the number of electrons. After getting the number of electrons, we can quickly write the electron configuration for oxygen. Now, orbitals can hold up to two electrons, so that we will put it after 1s. Next, we have the 2s; we will put two as well and have used four electrons. Now we have the 2p, and in the 2p, there are up to 6 electrons. Next, we need four to complete the notation for oxygen. Now we will just put a four after the 2p. If we add those numbers two plus two plus four, we will get eight which is the number of electrons for oxygen.

The ground-state electron configuration of Potassium

19 is the atomic number of potassium. Now we go down the first row, and we have 1s. Then we have 2s in the second row that can hold two electrons. Next, we go to the third row, and the first term is 2p. However, p orbitals can hold up to 6 electrons. So, we will put all 6 electrons in that 2p orbital. However, we have used a total of 10 electrons so far. Now we have 19 for potassium; also, in the third row, we have the 3s. Now, we will put two there and go for the next row, wherein the fourth row, we have 3p.
Next, we will put 6 electrons in the 3p; at this point, we have used 18 electrons. Now we only need one more to get to that 19. So after the 3p in the fourth row, we have that 4s turn. Next, all we need to do is put one electron there; 2 plus 2 plus 6 plus 2 plus 6 plus 1 gives us a total of 19 electrons. However, that is the ground-state electron configuration of potassium.