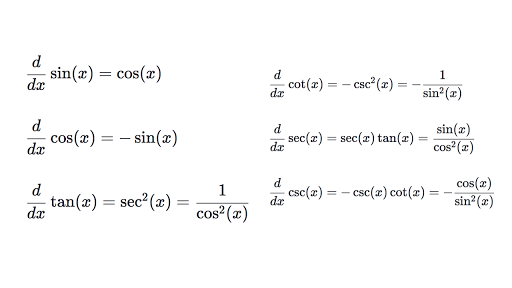Derivative and Tangent definition
What is Derivative
Let F be a real value function defined on an open interval (a,b). Now, it means the interval (a,b) is acting as the domain of F. However, the real value means the range of F is a subset of the collection of all drills.
Every small X sitting inside the open interval F of X exists. Now, this is the set of valid inputs for machine F. However, X exists to be a real number because F is real-valued. So, every X in the interval (a,b) of X exists to be a real number. However, (a,b) is the domain of all the points for which F is defined, and F of X is nothing but the real numbers range.
What is Tangent
A tangent of an angle is opposite over adjacent. However, the tangent is the one trig ratio that does not use the hypotenuse sign. However, a Tangent line is a line that is tangent to a curve. Now it means that it touches the curve at a single point. Then continues in either direction with precisely the slope of the curve at the point. However, the tangent line isn’t parallel to the curve itself; its slope just matches the slope of the specific point on the curve. However, the tangent line is beneficial because it can tell you the rate of change of a curve at a specific point.
Derivative of tangent X
- The connection between tangent x and cosines is that we can do right-hand genetics by saying x over cosine x. However, this is the same as taking sine x over cosine x. Next, The bottom function(g) is the first side which is cosine x. Then, the top function(f) is equal to sine x. However, the root of sine x is cosine x, so f is prime, which will be cosine x. Next, for the numerator, we will take cosine x, which is times with cos x. However, we need to subtract the cosine x times cosine and then the war potion rule. So, we need sine x times negative sine x.
- On the top, this cosine x times cosine x, which will be cosine squared x and minus sine x times negative sine x. Now we have two of the sciences multiplying; that’s why it’s sine squared x. However, one cosine squared x plus sine squared x is just one, so we have one on the bottom. Now, we have cosine x and then being square. However, that means it is cosine squared x. However, we know one over cosine means secant squared x.

Derivative of tangent Inverse
- The secant of X squared is equalled to the tangent of x. Now, y is equal to the inverse tangent of x, which is the same thing as saying that the tangent of y is equal to X. We need a derivative of both sides with respect to X.
- Now we need to apply the chain rule. Derivative of the tangent of y with respect to y is going to be secant squared of y. However, the cosine of y squared is the alike type function. When applying the chain rule, it’s going to be the derivative of the tangent of y with respect to y. Now, it times the derivative y with respect to x. On the right-hand side, the derivative of x with respect to x will be equal to one. Now we need to multiply both sides times the cosine of y squared. Then we get the derivative of y with respect to x equal to the y squared cosine. Let’s divide by one; the one is equal to the sine squared of y plus cosine squared of y.
- Now multiply one over the cosine and divide the numerator by the cosine square of y. Next, those characters are just going to have one. And the denominator is going to be equal to one. Then we are gonna have sine squared y over cosine squared y. However, this is the same thing as the sine of y over the cosine of y.
Answer
- Whole thing squared, which is one over one plus tangent of y square. Next this will be equal to one over one plus the tangent of y, which is equal to x squared. Now this is equal to one over one plus x squared.

Derivative of the tangent line
Tangent lines have been studied for more than 2000 years. However, a tangent line is a line that touches a circle at just one point. But over the centuries, this definition has been expanded to include lines touching other curves. When a line touches a circle at only one point, this is the tangent line. But a line that crosses a circle at two points, this is not a tangent line. However, this is a tangent line when a line touches the sine curve at the point over three square roots of three over two.
Equation of a tangent line
Q. Find the equation of tangent through P(3,4), a point on the circle 𝑥2+𝑦2 = 25
We have a circle x square plus y square equal 25 that means the radius should be five. Now the circle with origin at 0 and radius of five represented by x squared plus y squared equals 25. Then the point p has given to us in 3/4. So, we can plot that point on the circle, so it’s 3 and 4.
Slope of radius = y2-y1/x2-x1 = 4-0/3-0 = 4/3
Slope of tangent = -¾
Y = mx + b
4 = -¾ + b
4+9/4 = b
b= 25/4
y= -¾ × 25/4
4y = -3x + 25
3x + 4y – 25 = 0
Derivative of tangent squared.
- The tangent of x is a function, and we are squaring this function. Now we make u equal to tan of x. Then tangent squared of x is equal to the tangent of x. Now all squared, which is equal to u square. However, when it comes to differentiating a composite function of a function. Next we must apply the chain rule. Now, dy/dx is equal to dy/du by du/dx.
- In this case, the function y is equal to the tangent of x all squared. Another hand, dy/du is two u; we bring down the power of u and then subtract one from the power. Next, the du/dx is equal to the derivative of the tangent of x, equal to the secant squared of x. Now we have dy/dx equal two times u, which is the tangent of x by the secant squared of x. Next, the derivative commonly written as the derivative of the tangent squared of x is equal to 2 secants squared of x by the tan of x.
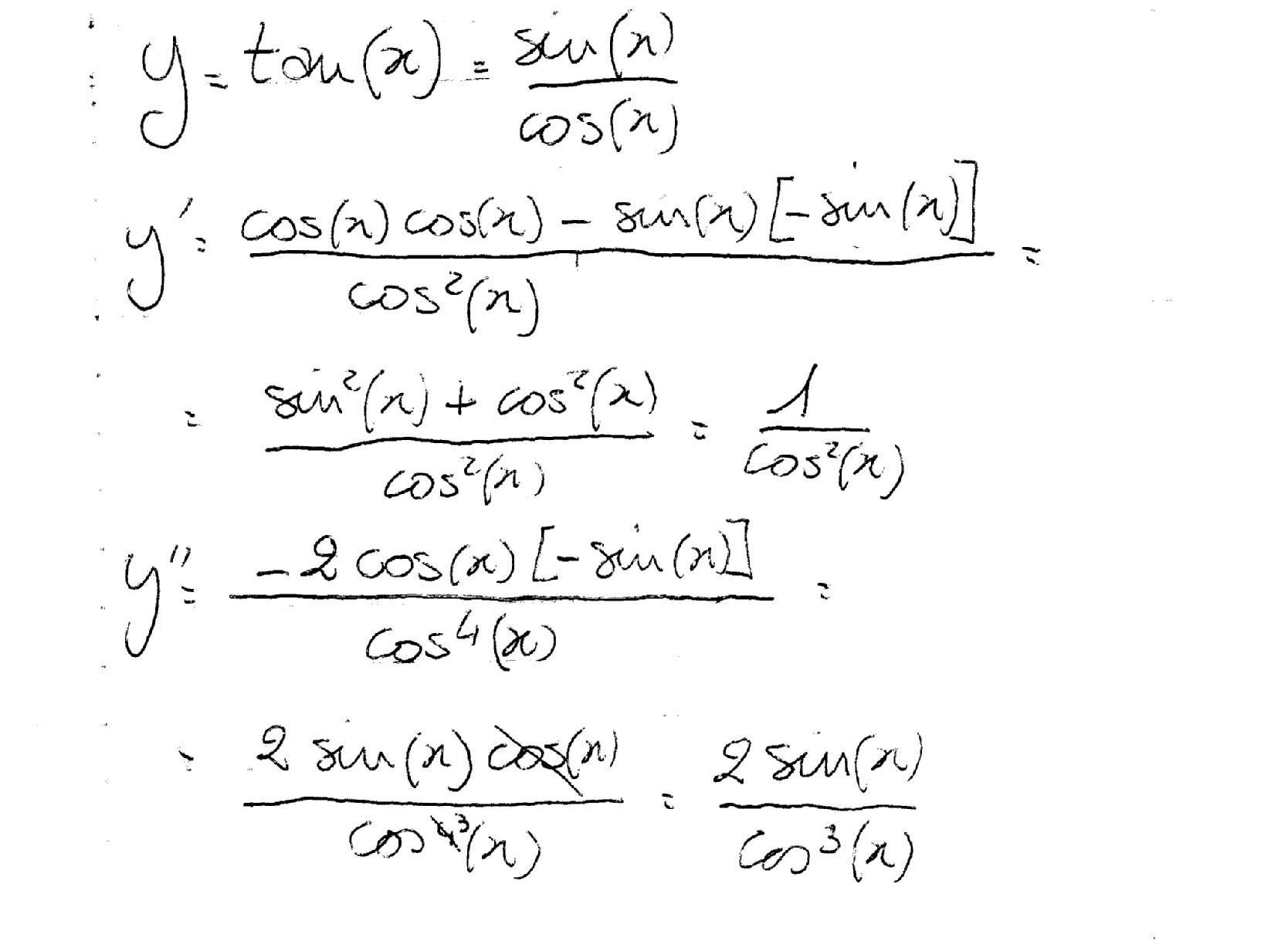
Derivative of trigonometric functions
- Derivative of sine x is equal to spine x.
- The derivative of cosine x is equal to negative sine x.
- The derivative of tangent x is equal to positive secant squared.
- Derivative of cosecant x is equal to negative cosecant x cotangent x.
- Derivative of secant x is positive secant x tangent x.
- The derivative of coltan x is negative cosecant square x.
Frequently asked questions
What is the Derivative of Tan x to x?
Positive secant squared is the derivative of tan x.
What is the tangent line formula?
y – y1 = m (x – x1) is the tangent line formula.
Is tangent the first derivative?
The first derivative of a function is the slope of the tangent line for any point on the function.