Logic in Geometry
Logic is a discovered skill; it’s miles as plenty a department of arithmetic as it’s miles a form of philosophy, or reasoning. Logic in geometry permits you to peer connections and patterns, to make leaps of information from the unmarried occasion to everyday truths.
Logic is an try to use strict regulations of questioning to attain dependable results, or conclusions, approximately claims, or premises. Here is a string of logical questioning:
If I take a look at each night time for 15 mins, then I could have a higher information of the geometry skills. If I even have a higher information of geometry, then I will earn better grades on assessments.
You can well summarize that through pronouncing that 15 mins of take a look at every night time can pay off in better grades in your geometry quizzes and tests.
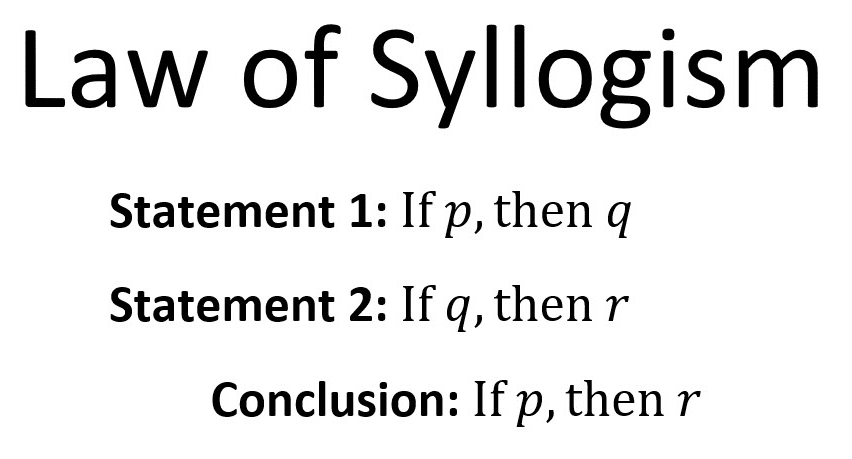
Syllogism Definition
Within common sense, numerous sorts of arguments, premises, and conclusions may be formed. A syllogism is a technique of reasoning through drawing a end from premises.
The precise sample of a syllogism is that the first, important premise stocks some thing with a second, minor premise, which in flip ends in a end, like this:
- I am creeped out, however additionally fascinated, through all spiders.
- That extensive tarantula is a spider.
- I am creeped out, however additionally fascinated, through that extensive tarantula.
Syllogism Examples
What is Truth?
A syllogism can gift defective premises. The end to any defective premise is mechanically invalid, like this instance:
- All animals have 4 legs.
- A snake is an animal.
- All snakes have 4 legs.
That makes no sense, because the important premise is wrong. Spiders have 8 legs; snakes have none; birds have . Anything constructed from that incorrect, important premise (that each one animals have 4 legs) is, then, invalid.
A syllogism also can have a defective end from legitimate premises. Look at this, and see the problem:
- Most human beings get frightened once they inform lies.
- You seem frightened.
- You have to be mendacity approximately some thing.
The important and minor premises are fine; maximum human beings genuinely do get frightened once they inform lies, and also you genuinely ought to seem frightened. But the belief is defective, due to the fact the minor premise can be defined through dozens of different things: you’re walking late; you dressed rapidly and your footwear do not match; your teach is deliberating benching you for the large game.
The Structure of a Syllogism
In a syllogism, the important premise is large and wide, like pronouncing, “All triangles have 3 facets and 3 indoors angles.” The important premise is frequently a conditional assertion, starting with “If.”
The minor premise scales down that premise to some thing local, exact, or familiar: “This is a 3-sided polygon.” It also can be a conditional assertion starting with “If.”
The end connects the everyday fact of the important premise to the instant instance of the minor premise: “Then this 3-sided polygon is a triangle.” Conclusions frequently start with “Then.”
The regulation of syllogism is likewise acknowledge as reasoning through transitivity. It is just like the transitive assets of equality, which says if this whatsit is like that doohickey, and that doohickey is like this thingamabob, then this whatsit is like this thingamabob:
- If a = b
- and if b = c
- then a = c
Taking the equal instance from in advance and recasting the premises as conditional statements, we ought to write:
- If all triangles have 3 facets and 3 indoors angles,
- And if that is a 3-side polygon,
- Then this 3-sided polygon is a triangle.
The regulation of syllogism affords for 2 conditional statements (“If …”) accompanied through a end (“Then …”). Logicians commonly assign letters to those elements of the syllogism:
Syllogism in Geometry Examples
The energy of common sense is visible again and again in geometric proofs. When you replacement terms, for instance, you’re following the regulation of syllogism:
- If ∠A is supplementary to ∠B
- and if ∠B = 115°
- then ∠A = 65°
Perhaps with out even noticing, you clear up many steps in geometric proofs the use of the regulation of syllogism. The regulation of syllogism directs you to apply deductive reasoning, which permits you to paintings right all the way down to particular examples from generalized postulates and theorems.